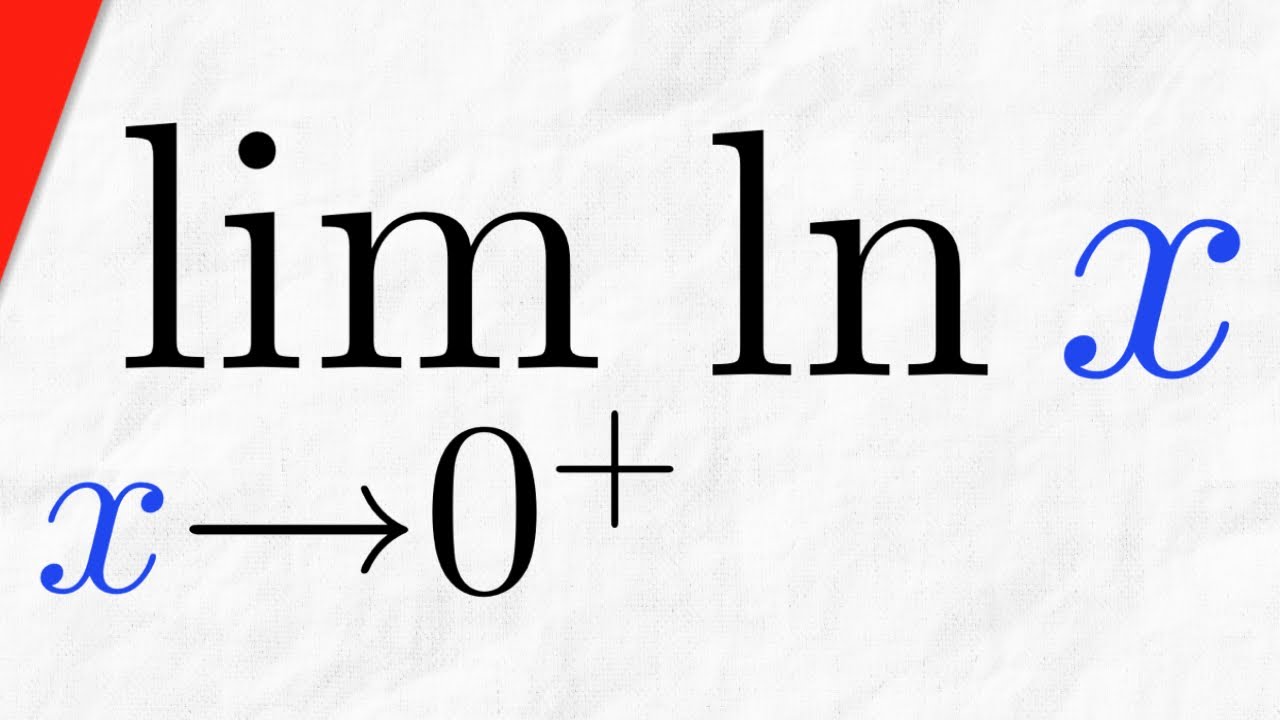An In-Depth Exploration Of "ln 0": Unraveling The Mysteries Of Logarithms

Understanding mathematical concepts can sometimes feel like deciphering a foreign language. Among these perplexing ideas is the logarithm, a fundamental concept within mathematics that serves as the backbone for many scientific calculations and theories. Within the realm of logarithms, the expression "ln 0" stands as a curious anomaly, sparking intrigue and debate among mathematicians and students alike. This article aims to demystify "ln 0" by delving into its mathematical significance, practical implications, and the underlying principles that govern its behavior.

Logarithms, introduced by John Napier in the early 17th century, revolutionized mathematical computations by transforming multiplicative processes into more manageable additive operations. The natural logarithm, denoted as "ln," is a specific type of logarithm with an important base – Euler's number (e), approximately equal to 2.71828. While logarithms like "ln 1" or "ln e" have clear and defined values, "ln 0" presents a unique challenge due to its undefined nature within the realm of real numbers. Understanding why "ln 0" is undefined requires a deeper exploration of logarithmic functions and their properties.

In this comprehensive article, we will embark on a journey through the world of logarithms, examining the theoretical and practical aspects of "ln 0" and its broader implications in mathematics and beyond. From the foundational principles of logarithms to the intriguing paradoxes they present, this piece will provide a thorough understanding of a concept that, while elusive, is integral to a wide array of scientific and mathematical disciplines. Prepare to engage with the intricacies of logarithms as we unravel the mysteries of "ln 0."

Table of Contents

• Understanding Logarithms
• The Nature of "ln 0"
• Mathematical Properties of Logarithms
• "ln 0" and Its Implications
• A Historical Perspective on Logarithms
• Applications in Science and Technology
• "ln 0" in Advanced Mathematics
• Common Misconceptions About "ln 0"
• Educational Approaches to Teaching Logarithms
• "ln 0" in the Context of Calculus
• "ln 0" and Complex Numbers
• "ln 0" in Computer Science
• "ln 0" and Logarithmic Scales
• Frequently Asked Questions
• Conclusion

Understanding Logarithms

Logarithms are a mathematical concept that allows us to explore the relationships between numbers in a multiplicative context. At its core, a logarithm answers the question: "To what power must a certain base be raised, to yield a specific number?" For example, in the expression log_b(x) = y, b is the base, x is the result, and y is the exponent or power. This relationship can be rewritten as b^y = x, showcasing the transformative power of logarithms to convert complex multiplicative operations into simpler additive ones.

The natural logarithm, denoted as "ln," is a specific type of logarithm that uses Euler's number (e) as its base. Euler's number is a transcendental number approximately equal to 2.71828, and it is fundamental to the field of calculus and complex analysis. The natural logarithm is particularly significant because it describes growth processes, such as exponential growth and decay, in a natural and intuitive way.

Logarithms are not just a theoretical construct; they have extensive applications in real-world scenarios. They are used in fields such as acoustics, where the decibel scale is logarithmic, and in finance, where compound interest calculations rely on logarithmic functions. Understanding logarithms is crucial for grasping the mathematical principles that underpin these diverse applications.

The Fundamental Properties of Logarithms

To fully understand logarithms, one must explore their fundamental properties. These properties include the product rule, the quotient rule, and the power rule:

• Product Rule: log_b(xy) = log_b(x) + log_b(y). This property shows that the logarithm of a product is the sum of the logarithms of the factors.
• Quotient Rule: log_b(x/y) = log_b(x) - log_b(y). This property demonstrates that the logarithm of a quotient is the difference between the logarithms of the numerator and the denominator.
• Power Rule: log_b(x^y) = y log_b(x). This property indicates that the logarithm of a power is the exponent times the logarithm of the base.

These properties highlight the versatility of logarithms in simplifying complex mathematical expressions. They also form the basis for more advanced logarithmic concepts and calculations.

The Nature of "ln 0"

The expression "ln 0" is a topic of considerable interest in mathematics due to its undefined nature within the realm of real numbers. To understand why "ln 0" is undefined, one must first appreciate the behavior of the natural logarithm function.

The natural logarithm function, ln(x), is defined for all positive real numbers x. Its graph is a continuous curve that approaches negative infinity as x approaches zero from the positive side (x → 0⁺). This behavior reflects the fact that there is no real number y such that e^y = 0, as Euler's number raised to any power is always positive. Consequently, "ln 0" does not exist within the real number system.

In mathematical terms, we express this by stating that the natural logarithm function has a vertical asymptote at x = 0. This means that as x approaches zero, the value of ln(x) decreases without bound, approaching negative infinity. Thus, "ln 0" is undefined because it lies outside the domain of the natural logarithm function.

Exploring the Limits of "ln 0"

To further explore the nature of "ln 0," we can examine the concept of limits. In calculus, the limit of a function describes its behavior as the input approaches a particular value. For the natural logarithm function, we can investigate the limit as x approaches zero from the positive side:

lim_{x → 0⁺} ln(x) = -∞

This limit expression formalizes the idea that as x gets closer and closer to zero, the value of ln(x) becomes increasingly negative, diverging towards negative infinity. This mathematical insight reinforces the notion that "ln 0" is undefined within the context of real numbers.

While "ln 0" is undefined in real numbers, it holds significance in other mathematical contexts, such as complex analysis, where it's explored through the concept of complex logarithms. In these advanced fields, the notion of "ln 0" can be extended and defined in ways that accommodate its otherwise elusive nature.

Mathematical Properties of Logarithms

Logarithms possess a rich set of mathematical properties that make them powerful tools in various calculations and problem-solving scenarios. Understanding these properties is essential for anyone seeking to harness the full potential of logarithms in mathematical and scientific contexts.

One of the most fundamental properties of logarithms is their ability to transform multiplication into addition. This property, known as the product rule, allows for the simplification of complex expressions. For example, consider the expression log_b(xy). Using the product rule, we can rewrite this as log_b(x) + log_b(y), making it easier to work with.

The Quotient and Power Rules

In addition to the product rule, logarithms also have the quotient rule and power rule, which are equally important for simplifying expressions:

• Quotient Rule: log_b(x/y) = log_b(x) - log_b(y). This property allows us to express the logarithm of a quotient as the difference between the logarithms of the numerator and the denominator.
• Power Rule: log_b(x^y) = y log_b(x). This property shows that the logarithm of a power is the exponent multiplied by the logarithm of the base.

Together, these properties form a comprehensive toolkit for working with logarithmic expressions, enabling mathematicians and scientists to tackle a wide range of problems with efficiency and precision.

Logarithms also exhibit a unique relationship with exponential functions. This relationship is encapsulated in the inverse property, which states that the natural logarithm of a number is the power to which e must be raised to yield that number. Mathematically, this is expressed as ln(e^x) = x and e^ln(x) = x for all positive real numbers x.

This inverse relationship is foundational to many applications of logarithms, particularly in calculus, where it plays a critical role in solving differential equations and modeling exponential growth and decay processes.

"ln 0" and Its Implications

The undefined nature of "ln 0" has far-reaching implications in mathematics and various scientific fields. Understanding these implications requires a deeper exploration of the role logarithms play in mathematical theory and practice.

One of the primary implications of "ln 0" is its impact on the domain of the natural logarithm function. As previously mentioned, the natural logarithm is defined only for positive real numbers. This restriction is due to the fact that Euler's number, e, raised to any power, is always positive, meaning that no real power of e can yield zero. Consequently, "ln 0" lies outside the domain of real numbers, reinforcing its undefined status.

Logarithmic Scales and Their Limitations

The undefined nature of "ln 0" also has practical implications for logarithmic scales, which are commonly used to measure quantities that span multiple orders of magnitude. Examples of logarithmic scales include the Richter scale for measuring earthquake intensity and the pH scale for assessing acidity and alkalinity.

In these scales, logarithms are used to compress large ranges of values into more manageable numbers. However, the undefined nature of "ln 0" means that these scales cannot accommodate zero values. For instance, on a logarithmic scale, a value of zero would correspond to negative infinity, making it impractical for measurement purposes.

This limitation necessitates careful consideration when using logarithmic scales, as they cannot represent zero or negative values. Instead, alternative approaches, such as shifting the scale or using a different mathematical framework, must be employed to handle such scenarios.

Despite these limitations, logarithmic scales remain invaluable tools for analyzing data and understanding relationships between variables, particularly in fields where exponential growth or decay is prevalent.

A Historical Perspective on Logarithms

Logarithms have a rich and storied history that dates back to the early 17th century. They were first introduced by the Scottish mathematician John Napier, whose work laid the foundation for the development of this transformative mathematical concept.

Napier's motivation for creating logarithms was to simplify complex calculations, particularly those involving multiplication and division. At the time, these operations were laborious and time-consuming, often requiring the use of cumbersome tables and manual calculations. By transforming multiplication into addition and division into subtraction, logarithms provided a more efficient and streamlined approach to mathematical computations.

Napier's Legacy and the Spread of Logarithms

Napier's introduction of logarithms was a groundbreaking achievement that quickly garnered attention throughout the mathematical community. His work was further developed and refined by other prominent mathematicians, including Henry Briggs, who introduced the concept of base-10 logarithms, known as common logarithms.

The widespread adoption of logarithms revolutionized the field of mathematics, making calculations more accessible and manageable. They became an essential tool for scientists, engineers, and astronomers, enabling them to tackle complex problems with newfound ease and precision.

Logarithms also played a pivotal role in the development of early calculating devices, such as the slide rule, which relied on logarithmic scales to perform arithmetic operations. These instruments were widely used for centuries until the advent of electronic calculators and computers.

Today, logarithms continue to be a fundamental component of mathematical education and scientific research, underscoring their enduring legacy and importance in the modern world.

Applications in Science and Technology

Logarithms are not merely abstract mathematical constructs; they have a wide array of applications in science and technology, where they are used to model and analyze complex systems and phenomena.

One of the most prominent applications of logarithms is in the field of acoustics, where they are used to measure sound intensity. The decibel scale, which quantifies sound levels, is a logarithmic scale that allows for the comparison of vastly different sound intensities in a manageable format. This scale is essential for understanding the dynamics of sound and its impact on human perception and health.

Logarithms in Finance and Economics

Logarithms also play a crucial role in finance and economics, where they are used to calculate compound interest and analyze investment growth. The compound interest formula, which determines the future value of an investment, relies on logarithmic functions to account for exponential growth over time.

This mathematical framework is invaluable for financial planning and decision-making, enabling individuals and businesses to assess the long-term potential of various investment strategies.

In addition to these applications, logarithms are used in fields such as chemistry, where they describe the behavior of chemical reactions, and in biology, where they model population dynamics and growth processes.

The versatility and utility of logarithms make them indispensable tools for scientists and researchers, facilitating the exploration and understanding of complex systems across diverse disciplines.

"ln 0" in Advanced Mathematics

While "ln 0" is undefined in the realm of real numbers, it holds significance in advanced mathematical fields such as complex analysis and calculus. These disciplines offer alternative perspectives and frameworks for understanding the behavior of logarithms in contexts where real numbers fall short.

In complex analysis, logarithms can be extended to complex numbers, allowing for the exploration of concepts such as the complex logarithm. This extension enables mathematicians to define "ln 0" in a way that accommodates complex values, providing a more comprehensive understanding of logarithmic behavior.

The Role of Logarithms in Calculus

Logarithms are also integral to calculus, where they serve as critical tools for solving differential equations and modeling dynamic systems. The natural logarithm, in particular, is used extensively in calculus to describe growth and decay processes, such as exponential growth and radioactive decay.

This mathematical framework is essential for understanding the behavior of functions and their derivatives, providing a foundation for more advanced calculus concepts and applications.

In summary, the exploration of "ln 0" and its implications in advanced mathematics underscores the depth and complexity of logarithmic functions, highlighting their significance in both theoretical and practical contexts.

Common Misconceptions About "ln 0"

The expression "ln 0" is often misunderstood due to its undefined nature within the realm of real numbers. Common misconceptions about "ln 0" stem from a lack of understanding of logarithmic functions and their properties.

One prevalent misconception is the belief that "ln 0" has a value of zero. This misunderstanding arises from a misinterpretation of the properties of logarithms, particularly the inverse relationship between logarithms and exponential functions. In reality, "ln 0" is undefined because no real power of Euler's number, e, can yield zero.

Misinterpretations of Logarithmic Scales

Another common misconception involves the use of logarithmic scales, where individuals may mistakenly assume that zero values can be represented on these scales. As previously discussed, logarithmic scales cannot accommodate zero or negative values, as these would correspond to undefined or negative infinity values, respectively.

To address these misconceptions, it is essential to provide a clear and accurate explanation of logarithmic functions and their properties, emphasizing the limitations and restrictions of logarithmic scales and expressions like "ln 0."

By fostering a deeper understanding of these concepts, educators and learners can overcome common misconceptions and appreciate the full potential of logarithms in mathematical and scientific contexts.

Educational Approaches to Teaching Logarithms

Teaching logarithms effectively requires a thoughtful and comprehensive approach that addresses the complexities and nuances of this mathematical concept. Educators can employ a variety of strategies to help students grasp the foundational principles and applications of logarithms, ensuring a thorough understanding of their significance.

One effective approach is to introduce logarithms through real-world applications, such as sound intensity measurements and financial calculations. By demonstrating the practical relevance of logarithms, educators can engage students and highlight the importance of mastering this concept.

Interactive Learning and Visualization Tools

Incorporating interactive learning tools and visualization techniques can also enhance students' understanding of logarithms. Graphing calculators, computer simulations, and online resources can provide dynamic visual representations of logarithmic functions, allowing students to explore their behavior and properties in a hands-on manner.

These tools can help students develop a more intuitive understanding of logarithmic concepts, such as the relationship between logarithms and exponential functions and the behavior of logarithmic scales.

Additionally, educators can encourage students to engage in collaborative problem-solving activities, where they work together to tackle logarithmic challenges and explore various approaches to finding solutions. This collaborative approach fosters critical thinking and encourages students to apply their knowledge in creative and innovative ways.

By adopting these educational strategies, educators can effectively teach logarithms and empower students to confidently navigate the complexities of this essential mathematical concept.

"ln 0" in the Context of Calculus

In the context of calculus, "ln 0" presents a unique challenge due to its undefined nature within the realm of real numbers. However, calculus offers a framework for exploring and understanding the behavior of logarithmic functions, including their limits and derivatives.

One of the key concepts in calculus is the limit, which describes the behavior of a function as its input approaches a particular value. In the case of the natural logarithm function, the limit as x approaches zero from the positive side is:

lim_{x → 0⁺} ln(x) = -∞

This limit expression formalizes the idea that as x gets closer and closer to zero, the value of ln(x) becomes increasingly negative, diverging towards negative infinity. This mathematical insight reinforces the notion that "ln 0" is undefined within the context of real numbers.

Differentiation and Integration of Logarithmic Functions

Logarithmic functions are also integral to the study of differentiation and integration in calculus. The derivative of the natural logarithm function, ln(x), is a fundamental concept that plays a critical role in solving differential equations and modeling dynamic systems:

d/dx [ln(x)] = 1/x

This derivative expression highlights the relationship between logarithmic functions and their rates of change, providing a foundation for more advanced calculus concepts and applications.

In addition to differentiation, integration involving logarithmic functions is a key area of study in calculus. The integration of ln(x) is expressed as:

∫ ln(x) dx = x ln(x) - x + C

This integral expression underscores the importance of logarithmic functions in calculus, where they are used to solve complex problems and model various phenomena.

In summary, the exploration of "ln 0" in the context of calculus highlights the depth and complexity of logarithmic functions, emphasizing their significance in both theoretical and practical applications.

"ln 0" and Complex Numbers

While "ln 0" is undefined in the realm of real numbers, it can be explored within the context of complex numbers, where it holds significance in complex analysis. This mathematical field offers an alternative perspective for understanding the behavior of logarithmic functions, providing a framework for defining "ln 0" in a way that accommodates complex values.

In complex analysis, the notion of the complex logarithm is introduced, allowing for the extension of logarithmic functions to the complex plane. This extension involves the use of complex numbers, which consist of both real and imaginary components, expressed in the form a + bi, where i is the imaginary unit.

The Complex Logarithm and Its Properties

The complex logarithm, denoted as Log(z), is a multi-valued function that can be expressed in terms of the complex exponential function:

Log(z) = ln|z| + iArg(z) + 2πik, where k is an integer, and Arg(z) is the principal argument of z.

This expression highlights the multi-valued nature of the complex logarithm, which arises due to the periodicity of the complex exponential function. The principal value of the complex logarithm is obtained by restricting the argument to a specific range, typically between -π and π.

The exploration of "ln 0" within the context of complex numbers underscores the depth and complexity of logarithmic functions, emphasizing their significance in both theoretical and practical applications.

By extending logarithms to the complex plane, mathematicians can gain a more comprehensive understanding of their behavior, providing insights into the nature of "ln 0" and its implications in advanced mathematical contexts.

"ln 0" in Computer Science

In the field of computer science, logarithms play a crucial role in various algorithms and data structures, where they are used to optimize performance and efficiency. The undefined nature of "ln 0" presents unique challenges and considerations for computer scientists, particularly in the context of numerical computations and algorithm design.

One of the primary applications of logarithms in computer science is in the analysis of algorithm complexity, where they are used to describe the growth rates of functions. The big O notation, which characterizes the upper bound of an algorithm's running time, often involves logarithmic expressions to represent logarithmic growth rates.

Logarithms in Data Structures and Algorithms

Logarithms are also integral to the design and implementation of data structures, such as binary search trees and heaps, where they are used to optimize search and retrieval operations. In these data structures, logarithmic time complexity is achieved by leveraging the properties of logarithmic functions, enabling efficient data access and manipulation.

Despite the challenges posed by the undefined nature of "ln 0," computer scientists can employ various strategies to handle scenarios involving zero or negative values. For example, numerical algorithms may incorporate error handling or approximation techniques to manage undefined expressions and ensure accurate and reliable results.

In summary, the exploration of "ln 0" in the context of computer science highlights the significance of logarithmic functions in algorithm design and performance optimization, emphasizing their importance in modern computing.

"ln 0" and Logarithmic Scales

Logarithmic scales are widely used in various scientific and engineering fields to represent quantities that span multiple orders of magnitude. These scales provide a way to compress large ranges of values into more manageable numbers, making them invaluable tools for data analysis and visualization.

The undefined nature of "ln 0" presents a unique challenge for logarithmic scales, as they cannot accommodate zero or negative values. In these scales, a value of zero would correspond to negative infinity, making it impractical for measurement purposes.

Applications of Logarithmic Scales

Despite this limitation, logarithmic scales remain essential for understanding relationships between variables and analyzing data in fields such as acoustics, where the decibel scale is used to measure sound intensity, and in seismology, where the Richter scale quantifies earthquake magnitude.

In these applications, logarithmic scales provide a framework for comparing vastly different quantities, allowing scientists and engineers to gain insights into the behavior and dynamics of complex systems.

To address the limitations of logarithmic scales, alternative approaches, such as shifting the scale or using a different mathematical framework, may be employed to handle scenarios involving zero or negative values. These strategies ensure that logarithmic scales remain a powerful and versatile tool for data representation and analysis.

Frequently Asked Questions

1. Why is "ln 0" undefined?

"ln 0" is undefined because the natural logarithm function is only defined for positive real numbers. There is no real number y such that e^y = 0, as Euler's number raised to any power is always positive.

2. How is "ln 0" explored in complex numbers?

In complex analysis, the complex logarithm is introduced, allowing for the extension of logarithmic functions to the complex plane. This extension provides a framework for defining "ln 0" in a way that accommodates complex values.

3. What are some applications of logarithms in computer science?

Logarithms play a crucial role in computer science, where they are used to analyze algorithm complexity, optimize data structures, and improve performance in various computational processes.

4. How do logarithmic scales work?

Logarithmic scales compress large ranges of values into more manageable numbers, allowing for the representation and comparison of quantities that span multiple orders of magnitude. They are commonly used in scientific and engineering fields for data analysis and visualization.

5. Can logarithmic scales accommodate zero values?

Logarithmic scales cannot accommodate zero or negative values, as these would correspond to undefined or negative infinity values. Alternative approaches, such as shifting the scale, may be employed to handle such scenarios.

6. What are some common misconceptions about "ln 0"?

Common misconceptions about "ln 0" include the belief that it has a value of zero and the assumption that zero values can be represented on logarithmic scales. These misunderstandings arise from a lack of understanding of logarithmic functions and their properties.

Conclusion

The exploration of "ln 0" offers a fascinating journey through the world of logarithms, revealing the depth and complexity of this mathematical concept. While "ln 0" is undefined within the realm of real numbers, its significance extends to advanced mathematical fields such as complex analysis and calculus, where it is explored through alternative perspectives and frameworks.

Logarithms play a crucial role in various scientific and technological applications, from acoustics and finance to computer science and data analysis. Understanding their properties and implications allows us to harness their full potential in mathematical and practical contexts.

By addressing common misconceptions and employing effective educational approaches, we can foster a deeper understanding of logarithms and empower learners to confidently navigate the complexities of this essential mathematical concept. Whether through real-world applications, interactive learning tools, or collaborative problem-solving, the study of logarithms remains a vital component of mathematical education and scientific inquiry.